Parallelogram law of forces

Parallelogram law of force enables us to determine the resultant force effective on a body when it is subjected to a system of force consisting of two forces.

This law states  that if two forces acting simultaneously be represented in magnitude and direction by the two adjacent  sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram drawn from the point of intersection of the two forces.

If two forces, represented by vectors  \(\overrightarrow{AB}\) and \(\overrightarrow{AD}\), acting under an angle θ  are applied to a body at point A, their action is equivalent to the action of one force, represented by the vector \(\overrightarrow{AC}\), obtained as the diagonal of the parallelogram constructed on the vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AD}\) and directed as shown in the figure

Let us consider a parallelogram  ▱ABCD. Two forces \(\mathbf{\vec{P}}\) and \(\mathbf{\vec{Q}}\) be represented by the two sides of the parallelogram AB and AD respectively and the resultant force \(\mathbf{\vec{R}}\) is represented by the diagonal AC.

The force \(\vec{R}\) is called the resultant of the two forces \(\vec{P}\) and \(\vec{Q}\). The forces P and Q are called components of the force R. Thus a force is equivalent to its components, and vice versa.

Let’s extend the line AB and draw a perpendicular line CE on the extension of the line AB .

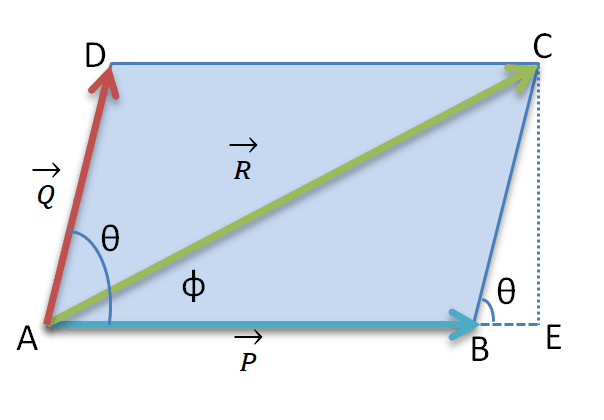
From traingle \(\triangle BCE\), we can write  Sin θ= \(\frac{CE}{BC}\)

                                                           Or, CE= BC Sin θ

and again we can write  Cos θ= \(\frac{BE}{BC}\)

                                                           Or, BE= BC Cos θ

Now  from traingle  \(\triangle ACE\), we can write   

AC²=AE² + CE²

AC²=(AB+BE)² + CE²   

or, AC²= (AB+ BC cos θ)² + (BC sin θ)²

or,R²= (P+Q cos θ)²+ Q²sin²θ              [As AB= P, AD=BC=Q, and AC= R]

or, R²= P² +2PQcosθ+Q²cos² θ + Q²sin²θ

or, R²= P²  +Q²(cos² θ+sin²θ) +2PQcosθ

or, R²= P² + Q² +2PQcosθ                 (as cos² θ+sin²θ = 1) …….(i)   

            ^{R = \(\sqrt{P^{2}  + Q^{2} +2PQcosθ }\)}

Direction :   

Let’s assume the resultant force R is acting at an angle φ with the force P

Now  from  triangle  \(\triangle ACE\), we can write tanφ = \(\frac{CE}{AE}\)

Or,  tanφ = \(\frac{CE}{AB + BE}\)

Or,  tanφ = \(\frac{BCsinθ}{AB + BCcosθ}\)

              tanφ = \(\frac{Qsinθ}{P + Qcosθ}\)                         (As BC= Q )

Conditions: 

• When θ =0° ; when two forces are collinear and are in the same direction.

from equation (i) we get, R²= P² + Q² +2PQcosθ  

R²= P² + Q² +2PQ    (as cos0° =1) 

R²= (P+Q)²

      ∴ \(R_{max}\)=P+Q

• When θ =180° ; when two forces are collinear and are in the opposite direction.

from equation (i) we get, R²= P² + Q² +2PQcosθ  

R²= P² + Q² -2PQ    (as cos180° =-1) 

R²= (P-Q)²

      ∴ \(R_{min}\)=P-Q

• When θ =90° ; when two forces are normal to each other.

from equation (i) we get, R²= P² + Q² +2PQcosθ  

R²= P² + Q²     (as cos90° =0) 

    ∴ R= \(\sqrt{P^{2} +Q^{2}}\)